C++ Neural Networks and Fuzzy Logic by Valluru B. Rao M&T Books, IDG Books Worldwide, Inc. ISBN: 1558515526   Pub Date: 06/01/95

Pre processing the Data for the Network

Surprising as it may sound, you are most likely going to spend about 90% of your time, as a neural network developer, in massaging and transforming data into meaningful form for training your network. We actually defined three substeps in this area of preprocessing in our master list:

•  Highlight features

•  Transform

•  Scale and bias

Highlighting Features in the Input Data

You should present the neural network, as much as possible, with an easy way to find patterns in your data. For time series data, like stock market prices over time, you may consider presenting quantities like rate of change and acceleration (the first and second derivatives of your input) as examples. Other ways to highlight data is to magnify certain occurrences. For example, if you consider Central bank intervention as an important qualifier to foreign exchange rates, then you may include as an input to your network, a value of 1 or 0, to indicate the presence or lack of presence of Central bank intervention. Now if you further consider the activity of the U.S. Federal Reserve bank to be important by itself, then you may wish to highlight that, by separating it out as another 1/0 input. Using 1/0 coding to separate composite effects is called thermometer encoding.

There is a whole body of study of market behavior called Technical Analysis from which you may also wish to present technical studies on your data. There is a wide assortment of mathematical technical studies that you perform on your data (see references), such as moving averages to smooth data as an example. There are also pattern recognition studies you can use, like the “double-top” formation, which purportedly results in a high probability of significant decline. To be able to recognize such a pattern, you may wish to present a mathematical function that aids in the identification of the double-top.

You may want to de-emphasize unwanted noise in your input data. If you see a spike in your data, you can lessen its effect, by passing it through a moving average filter for example. You should be careful about introducing excessive lag in the resulting data though.

Transform the Data If Appropriate

For time series data, you may consider using a Fourier transform to move to the frequency-phase plane. This will uncover periodic cyclic information if it exists. The Fourier transform will decompose the input discrete data series into a series of frequency spikes that measure the relevance of each frequency component. If the stock market indeed follows the so-called January effect, where prices typically make a run up, then you would expect a strong yearly component in the frequency spectrum. Mark Jurik suggests sampling data with intervals that catch different cycle periods, in his paper on neural network data preparation (see references ).

You can use other signal processing techniques such as filtering. Besides the frequency domain, you can also consider moving to other spaces, such as with using the wavelet transform. You may also analyze the chaotic component of the data with chaos measures. It’s beyond the scope of this book to discuss these techniques. (Refer to the Resources section of this chapter for more information.) If you are developing short-term trading neural network systems, these techniques may play a significant role in your preprocessing effort. All of these techniques will provide new ways of looking at your data, for possible features to detect in other domains.

Scale Your Data

Neurons like to see data in a particular input range to be most effective. If you present data like the S&P 500 that varies from 200 to 550 (as the S&P 500 has over the years) will not be useful, since the middle layer of neurons have a Sigmoid Activation function that squashes large inputs to either 0 or +1. In other words, you should choose data that fit a range that does not saturate, or overwhelm the network neurons. Choosing inputs from –1 to 1 or 0 to 1 is a good idea. By the same token, you should normalize the expected values for the outputs to the 0 to 1 sigmoidal range.

It is important to pay attention to the number of input values in the data set that are close to zero. Since the weight change law is proportional to the input value, then a close to zero input will mean that that weight will not participate in learning! To avoid such situations, you can add a constant bias to your data to move the data closer to 0.5, where the neurons respond very well.

Reduce Dimensionality

You should try to eliminate inputs wherever possible. This will reduce the dimensionality of the problem and make it easier for your neural network to generalize. Suppose that you have three inputs, x, y and z and one output, o. Now suppose that you find that all of your inputs are restricted only to one plane. You could redefine axes such that you have x’ and y’ for the new plane and map your inputs to the new coordinates. This changes the number of inputs to your problem to 2 instead of 3, without any loss of information. This is illustrated in Figure 14.1.

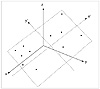
Figure 14.1  Reducing dimensionality from three to two dimensions.